无向图的操作比较有向图而言,可能比较复杂,但是算法的基本原理可以说是相通的,都是邻接表操作(上文的十字链表可以看作特殊的邻接表)
“邻接表”
抽象数据类型比较“十字链表”较为简单,头节点,弧节点的数据类型定义如下:
typedef struct UDG_ArcNode {
int adjvex;
struct UDG_ArcNode* nextarc;
UDG_InfoType *info;
}UDG_ArcNode;
typedef struct UDG_VNode {
UDG_VertexType data;
UDG_ArcNode* firstarc;
}UDG_VNode,AdjList[UDG_MAX_VERTEX_NUM];
typedef struct {
AdjList verticles;
int vexnum, arcnum;
int kind;
}ALGraph;同上篇,为每个头节点(顶点)建立一个单链表,根据头节点可以依次访问每一个顶点的“域”信息,而多个链表组合,即为图结构(U-D-G)
创建一个无向图:

依据邻接表的抽象数据定义:
假设以A为第一链表头节点,则,D\C\B为顺时针的“邻居”,头指针指向A,则A的指向第一条依附于该点的弧指针应当指向10,10的指向下一条弧的指针应当指向28,依次类推,28指向45
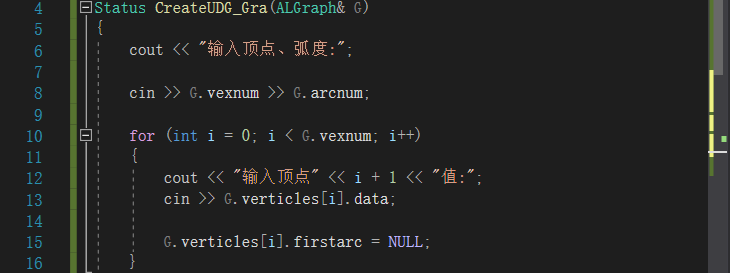
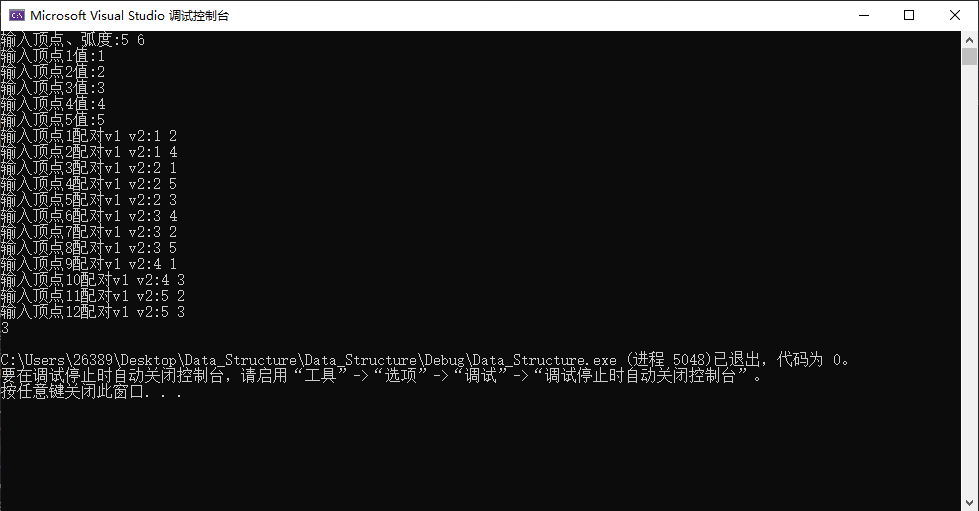
1.输入顶点和节点数
2.为顶点赋值,并且为其指向弧的指针初始化为空值
[PS]:默认顶点位置为其值减一,顶点位置连续[0,1,2,……]
for (int k = 0; k < G.arcnum*2; k++)
{
cout << "输入顶点" << k + 1 << "配对v1 v2:";
int v1, v2;
cin >> v1 >> v2;
int m = v1 - 1, n = v2 - 1;
UDG_ArcNode* p;
p = (UDG_ArcNode*)malloc(sizeof(UDG_ArcNode));
*p = {n,G.verticles[m].firstarc,NULL};
G.verticles[m].firstarc = p;
}利用上述循环建立图,注意一下:
1.循环次数为弧数的2倍(C-r-e)
2.输入配对点并默认位置
3.建立节点(弧)
4.节点赋值
注意节点赋值循环问题,假设以遍历一个顶点的所有弧为例,若以顺时针输入依次的配对点,以上图为例:
则以此为(A点为例):AD\AC\AB
下面开始走一遍一个顶点的链表的程序流程:

- 输入A\D
- 获取A\D位置
- 建立弧节点
- 弧节点赋值与头节点指向([空值,A->10]—>[10,A->28]—>[28,A->45])
一轮单顶点链表建立结束(顺序实际上也很重要,对访问单个值而言,但是,遍历则无关紧要)
有意思的是:
上述的赋值操作,顺时针输入,最后变成了逆时针指向AB\AC\AD🤣
测试正确性操作: